94.386 Umdrehungen
oder Wie bestimme ich den Erdumfang?
Weiter schauen, schneller messen, besser abbilden ist das Ziel der meisten Amateure. Bei der Beobachtung immer nur auf neue technische Hilfsmittel setzen ist spannend, dabei geht leider ein wenig vom "Erlebnis Astronomie" verloren. Wo ist der Unterschied, ob ich ein CCD-Bild von einem Roboterteleskop aus dem Internet sauge oder von der Astro-CD lade? Um mir ein wenig von der Begeisterung der Astronomie zu erhalten, habe ich ein Projekt gesucht, bei dem ich sowohl ein (Meß)Ergebnis erreiche und mit möglichst wenig Technik auskomme.
Wer den ganzen Tag vor dem Bildschirm sitzt und Bilder bearbeitet hat wenig Lust, sich auch in der Freizeit mit elektronischer Bildverarbeitung zu befassen. So brauchte ich ein neues Projekt, bei dem ich mein Hobby Astronomie betreiben kann. Fast alle ernsthaften Beobachtungen sind mit hohem technischen oder zeitlichen Aufwand verbunden. Gibt es nicht vielleicht doch ein Gebiet, wo mit wenig Einsatz viel erreichen ist? Gerade in der Astronomie als älteste Wissenschaft sollte sich eine kleine Nische finden lassen. Wie wäre es wenn ich ganz ganz vorne anfange und versuche die wichtigsten astronomischen Zahlen zu bestimmen?
Die Aufgabe hört sich leichter an, als sie ist. Denn während die antiken Astronomen auf sehr alte Aufzeichnungen zurück greifen konnten, haben wir keine langen Meßreihen mit Instrumenten, wie sie die antiken Astronomen benutzten. Bei allen Messungen müssen wir von Null beginnen.
Welche Größen können wir in relativ kurzer Zeit bestimmen? Fast jedes Buch zur Geschichte der Astronomie erwähnt, daß Eratothenes (276-192 B.C.) als Erster den Erdumfang mit annehmbaren Genauigkeit vermessen hat. Eratothenes ist nicht der Erste, der von der Kugelgestalt der Erde sprach und auch nicht der Erste, der einen Wert für den Erdumfang angab, bei allen früheren Autoren ist jedoch nie angeben, wie der Wert ermittelt wurde.
Bevor ich mit dem Messen anfange, muß ich wissen, welche Hilfsmittel ich benutzen darf und welches Wissen ich verwenden kann. Für meinen ersten Versuch schränkte ich meine Auswahl nur wenig ein. Eine wichtige Freiheit, die ich mir nahm, war es alles Wissen, das mir heute zur Verfügung steht zu benutzen. Als mechanische Hilfsmittel gestattete ich alles, was man auch vor 2000 hätte bauen können.
Nun wie vermißt man die Erde? Eine Annahme, die die Griechen schon recht früh getroffen haben ist, daß die Erde eine Kugel ist. Wenn man weiter vermutet, daß die Sonne sehr weit entfernt von der Erde ist, kann man sich leicht eine geometrische Konstruktion zur Bestimmung des Erdradius vorstellen. Wenn die Entfernung von zwei Punkten auf der Kugeloberfläche bekannt ist und der zugehörige Winkelabstand, läßt sich sofort der Umfang und dann der Radius bestimmen. Eine allgemeine Messung des Winkelabstandes auf der Erde ist sehr schwer. Mißt man auf einem Meridian zur gleichen Zeit die Höhe eines im Süden stehenden Objekts über dem Horizont, ergibt die Differenz der Höhen genau den Winkelabstand der Orte auf der Erdoberfläche.
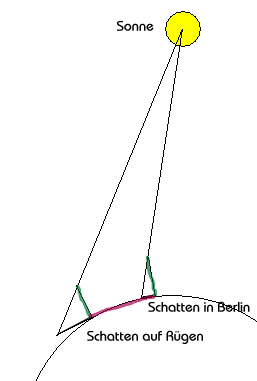
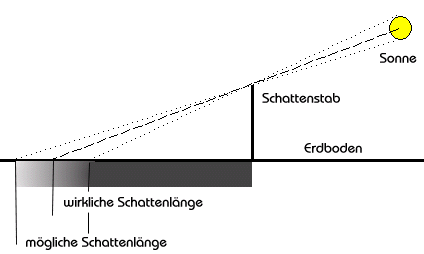
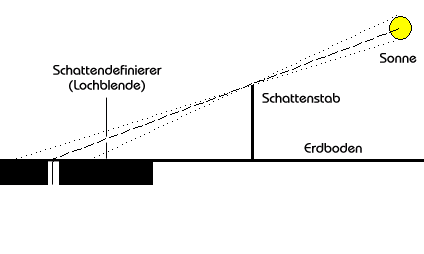
Ein Stern ist ein günstiges Beobachtungsobjekt, doch ohne Fernrohr ist eine genaue Bestimmung der Höhe recht schwierig. Mit einem Schattenmesser, auch Gnomon genannt, kann man die Höhe der Sonne sehr genau bestimmen. Leider gibt es ein kleines Problem. Die Sonne ist keine Punktlichtquelle und so ist der Schatten der Sonne nicht scharf begrenzt. Mit einer Erfindung, die schon vor weit mehr als 2000 in China gemacht wurde, kann man den Schatten schärfen. In den Strahlengang zwischen dem Schattenstab und der Skala wird ein Metallplättchen mit einem sehr kleinen Loch eingebracht.
Wie ich den Winkel zwischen den beiden Orten bestimmen kann ist nun bekannt, jetzt muß ich nur noch die Nord-Südentfernung messen. Als Strecke wählte ich Berlin-Peenemünde (auf Usedom). Die Berliner Sternfreunde verbringen dort jedes Jahr im Sommer eine Woche mit Beobachtungen.
Bei der Wahl der Strecke war für mich wichtig, daß die Straßen möglichst Nord-Süd verlaufen, damit ich nicht so viel messen muß und daß die Straßen möglichst wenig mit Autos befahren sind. Meine Fahrt begann in Bernau, einem Endbahnhof der S-Bahn nördlich von Berlin. Von dort führt der Weg auf sehr gut ausgebauten Waldwegen nach Zühlsdorf. Schon auf dieser Strecke wurde mir klar, wie schwierig die Messung ist. Plötzlich merkte ich, wie viele Kurven eine scheinbar gerade Straße hat. Jedes Anhalten und wieder Anfahren kostet viel Kraft. Der Kompaß reagiert sehr empfindlich auf meinen Drahtesel und so mußte ich für jede Messung absteigen und mich mehrere Meter vom Rad entfernen.
Bald wurde ich müder und begann kleinere Kurven nicht mehr zu vermessen. Meine Hoffnung war, daß sich die Fehler der einzelnen Strecken wunderbar wegmitteln werden. Über Zehdenick, Templin, Woldegk, Friedland ging es auf kleinen fast unbefahrenen Straßen nach Norden. In den Ortschaften hatte ich die meisten Probleme mit der Messung. Die Straße schlägt fast immer eine oder zwei größere Kurven, so daß ich am Ende des Ortes nicht mehr wußte, ob die Richtung stimmt. Eine Messung im Ort war deutlich zu aufwendig, denn ich hätte alle 100 Meter absteigen müssen.
In Friedland wurde die Entscheidung schwierig. Soll ich 30 km Bundesstraße fahren oder mich eine fast doppelt so weite Strecke auf kleinen Waldwegen durchschlagen? Mittlerweile recht müde nach 1?? Km Fahrt entschied ich mich für die Bundesstraße. Der beginnende Regen veranlaßte mich jedoch bald zur Schlafplatzsuche.
Am nächsten Morgen ging es weiter nach Anklam. Die Straße nach Wolgast und weiter nach Peenemünde war wieder gut befahrbar. Nach einer weiteren langen Regenpause kam im Lager der Sternfreunde am Peenemünder Strand an. Leider war das Wetter die ganzen folgenden Tage sehr durchwachsen, so daß ich keine Mittagshöhe der Sonne bestimmen konnte.
Für die Auswertung der Meßwerte benutzte ich natürlich den Computer. Nach drei Stunden am Rechenknecht, war der erste Teil der Auswertung fertig. Wenn ich den Winkelabstand zwischen Bernau und Peenemünde aus der Karte ablas, ergab sich ein fast perfekter Erdduchmesser. Nun fehlt mir nur die Sonnenstandshöhe an beiden Orten. Für diesen Zweck bastelte ich mir einen Schattenzeiger mit einem ca. 1 Meter langen Schattenstab. Mit Hilfe des chinesischen Schattenschärfers wird der Schatten so scharf, daß die Schattenlänge millimetergenau bestimmt werden kann.
An mehreren Tagen im September bestimmte ich in Berlin die Mittagshöhe der Sonne. An insgesamt fünf Meßtagen wich meine Sonnenhöhe nur 0.05 Grad von dem im Ahnert gegebenen Wert ab.
Nun konnte ich abschätzen, wie groß meine Erde wird. Von Bernau bin ich 94386 Radumdrehungen nach Peenemünde gefahren, 79155 davon nach Norden. Als Winkelabstand muß ich einen Wert von 1,5 Grad schätzen. Für die ganze Erde werden es fast 19 Millionen Umdrehungen meines Vorderrades (für Leute, die noch in Kilometer messen, hat die Erde einen Umfang von ~ 41.000 km)
Für den ersten Versuch bin ich mit dem Ergebnis sehr zufrieden. Doch nicht ganz, denn ich habe nicht exakt die historischen Bedingungen eingehalten. Beim nächsten mal werde ich auf den Kompaß verzichten und testen, wie genau eine relative Winkelmessung auf einer solchen Strecke erfolgen kann. Wenn ich etwas Glück habe, kann ich echte Meßwerte für die Sonnenstandshöhe in zwei Orten gewinnen.
PS:
Ich bin nicht der einzigste, der so was tut, ein interesantes Schülerprojekt finden Sie bei
Noon-Projekt.
letzte Änderung am 26. Oktober 2003
Kommentare, Fragen etc an: davidi@sternklar.de